随机算法：算法步骤往往非常简单，但是要验证其有效性，需要很多数学知识。往往实现简单，但是设计复杂。

这个学期的『随机算法』课程收获非常大，不仅巩固了之前所学的算法知识，还对复杂度分析、概率论都有了更加深入的了解，还学习到了利用随机性打破复杂问题求解的下界的方法。在准备考试的同时，写下这篇文章留给读者和未来的自己看，希望能让大家有所收获。

CNF、DNF、k-SAT 问题、MAX-SAT 问题、DNF 满足性赋值

名词解释

这些名词在『数理逻辑』课程中有过深入的学习，如需深入了解，可阅读《数理逻辑引论》。

CNF (Conjunctive normal form) 中文名叫做『合取范式』，『合』就是『and』的意思（与之相对，『析』就是『or』的意思），合取范式由一系列析取式作合取而得到，比如下面的几个都是合取范式：

$\begin{aligned} & {\displaystyle (A\lor \neg B\lor \neg C)\land (\neg D\lor E\lor F)} \\ & {\displaystyle (A\lor B)\land C} \\ & A\lor B \\ & A \\ & C_1 \land C_2 \land \cdots \land C_m (C_i 为析取式) \end{aligned}$

DNF (Disjunctive normal form) 中文名叫做『析取范式』，例子如下：

$\begin{aligned} & {\displaystyle (A\land \neg B\land \neg C)\lor (\neg D\land E\land F)} \\ & {\displaystyle (A\land B)\lor C} \\ & {\displaystyle A\land B} \\ & {\displaystyle A} \\ & D_1 \lor D_2 \lor \cdots \lor D_m (D_i 为合取式) \end{aligned}$

k-SAT 问题 (k-satisfiability problem)：CNF 需要每个析取子句都为真，最终才为真。k-SAT 问题是说，每个析取子句的长度都不超过 $k$，算法输出是否存在使得 CNF 为真的对变量的赋值，是的话输出一种赋值。一个例子如下：

$\begin{aligned} & 输入：x_1 \lor \lnot x_3, \lnot x_2 \lor x_3 , \lnot x_1 \lor \lnot x_2 , x_2 \lor x_3 \\ & 输出：\text{Yes} (x_1=T, x_2=F, x_3=T) \end{aligned}$

MAX-SAT 问题也是针对 CNF 的，只不过不是要 CNF 为真，因为这往往是很难实现的，而只是要输出使得 $C_1, \cdots, C_m$ 被同时满足的子句最多的变量赋值。同样 MAX-k-SAT 就是要求每个析取子句的长度不超过 $k$。

在 k-SAT 返回 Yes 和使 CNF 为真的解时，MAX-k-SAT 也会返回使 CNF 为真的解，在 k-SAT 返回 No 时，MAX-k-SAT 会返回使 CNF 的析取子句被满足数量最多的解。因此可以认为 MAX-k-SAT 包含了 k-SAT 问题，k-SAT 问题比 MAX-k-SAT 问题更加容易求解。

一个看起来很假的算法：

显然，得到正确解的概率是很低的，后续我们会对这个算法进行数学分析，再做一些优化。

DNF 满足性赋值：DNF 只需要一个合取子句为真，最终的结果就为真。DNF 满足性赋值要求输出能够使 $D_1, \cdots, D_m$ 之一满足的变量赋值。其实 SAT 问题既可以针对 CNF，也可以针对 DNF，我这里沿用老师在课堂上的讲法，将 SAT 问题专门用来分析 CNF 赋值问题，DNF 赋值问题用『DNF 满足性赋值』这个术语。

2-SAT 随机赋值算法

算法的思想非常简单，随机选定一个赋值，不满足的话就修改未被满足的子句的一个变量：

下面我们将证明，在循环次数为 $N = 2kn^2$ 的情况下，算法找到正确解的概率至少为 $1-1/2^k$。这样算法的时间复杂度就是 $O(2kmn^2)$，是多项式时间的算法，老师提到 2-SAT 问题也存在确定的多项式时间的算法，但是比较复杂，课堂上没有进行讲解。

证明思路：

1. 将第 7 步修改的过程抽象为随机游走，建立从『任意赋值』到『使范式为真的赋值』所需的步数与 $n$ 的数学关系。
2. 评价算法得到解得概率。

我们不妨假设 CNF 有一解 $S$，算法在循环的过程中，第 $i$ 轮产生的变量赋值为 $A_i$，如下图所示：

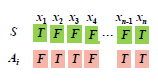
定义随机变量 $X_i$ 表示 $x_1, \cdots, x_n$ 在 $A_i$ 与 $S$ 中取值一致的变量个数。$X_i=n$ 表明 $A_i=S$，算法将终止。

对第 7 步进行分析，我们可以得出 $X_{i+1}$ 与 $X_i$ 的数学关系：

1. 若 $X_i=0$，即 $A_i$ 与 $S$ 对每一个变量的赋值都不同，则不管修改哪一个变量 $x_k$，都会变成和 $S$ 中对 $x_k$ 的赋值一样，则 $X_{i+1}=1$。
2. 若 $X_i \neq 0$，要进一步分情况讨论，我们不妨表示 $C_j=x_{j1} \lor x_{j2}$：
   1. 事件 $A$: 如果 $X_i$ 对 $x_{j1}, x_{j2}$ 的赋值与 $S$ 都不同，则 $X_{i+1}=X_i+1$；
   2. 事件 $B$: 如果 $X_i$ 对 $x_{j1}, x_{j2}$ 的赋值与 $S$ 只有一个不同，则 $X_{i+1}=\begin{cases} X_i+1, P = 1/2 \\ X_i-1, P = 1/2 \\ \end{cases}$

综上所述，看起来 $X_{i+1}=X_i+1$ 的概率比 $X_{i+1}=X_i-1$ 要大一些，简单地证明一下：

$\begin{aligned} P(X_{i+1} = X_i +1) &= P(X_i=0)P(X_{i+1}=X_i+1|X_i=0) + P(X_i\neq 0)P(X_{i+1}=X_i+1|X_i\neq 0) \\ &= P(X_i=0) + P(X_i\neq 0) [P(A|X_i\neq 0) + P(B|X_i\neq 0) \frac{1}{2}] \\ &\ge P(X_i=0) + P(X_i\neq 0) [P(A|X_i\neq 0) \frac{1}{2} + P(B|X_i\neq 0) \frac{1}{2}] \\ &= P(X_i=0) + P(X_i\neq 0) \frac{1}{2} \\ &\ge P(X_i=0)\frac{1}{2} + P(X_i\neq 0) \frac{1}{2} \\ &= \frac{1}{2} \end{aligned}$

同理可证明，$P(X_{i+1}=X_i-1) < \frac{1}{2}$。

这样，可以得到如下图所示的马尔科夫链：

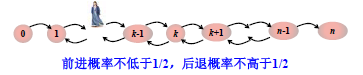
$X_i \in [0, n]$，考虑最坏情况，$X_0=0$，即 $A_i$ 与 $S$ 完全不同，那么从状态 $0$ 到达状态 $n$ 需要多少步？给定步数，不能到达状态 $n$ 的概率又是多少？下面来进行分析。首先，为了简化问题，认为前进后退概率均为 $\frac{1}{2}$。

令 $h_k$ 表示从状态 $k$ 到达状态 $n$ 需要的时间的随机变量，下面求解 $E(h_0)$。

因为从状态 $k$ 到状态 $n$ 要么经过 $k-1$（$k=0$ 时除外），要么经过 $k+1$，所以：

$h_k = \begin{cases} h_k+1, P = \frac{1}{2} \\ h_k-1, P = \frac{1}{2} \end{cases}$

有：

$E(h_k) = 1+\frac{E(h_{k-1})}{2}+\frac{E(h_{k+1})}{2}$

归纳可证：$E(h_k)=E(h_{k+1})+2k+1$。

另外两个特殊情况：

$\begin{aligned} & h_0 = 1+h_1 \\ & h_n=0 \end{aligned}$

均值：

$E(h_0) = E(h_1+1) = E(h_1)+1=E(h_2)+3 = \cdots = 1+3+5+\dots+(2n-1)+0=n^2$

也就是说，从状态 $0$ 到状态 $n$ 平均需要 $n^2$ 步，再根据 Markov 不等式可知，经过 $2n^2$ 步，仍然没有到达状态 $n$ 的概率小于 $1/2$：

随机算法这门课经常就是这样的套路：

1. 计算所需运行次数均值
2. 利用 Markov、Chebyshev、Chernoff 界算一个给定运行次数之下仍然得不到解的尾概率
3. 重复算法多少遍，错误概率缩小，正确概率放大

$P(h_0 \ge 2n^2) \le \frac{E(h_0)}{2n^2} = \frac{1}{2}$

况且，我们是按照前进概率『等于』后退概率算的，如果前进概率大于后退概率，所需的平均步骤更少。还有，我们是按照状态 $0$ 为开始状态算的，这是最坏的开始情况。因此，我们可以得到：从任意布尔赋值开始，运行 $2n^2$ 遍仍未找到满足性赋值的概率不超过 $\frac{1}{2}$。

接下来重复算法 $k$ 次，全都得不到解的概率不超过 $\frac{1}{2^k}$，能够得到解得概率至少为 $1-1/2^k$。

3-SAT 随机算法

不同于 2-SAT，3-SAT 目前还未找到多项式时间的确定性算法，属于 $NP$ 问题。

3-SAT 如果还是用原来的 2-SAT 算法这个过程，那么算出来的从 $0$ 到 $n$ 的期望步数为 $E=(h_0) 2^{n+2}-3n-4$（前进概率 $1/3$，后退概率 $2/3$），而布尔赋值总共才只有 $2^n$ 种，必须改进。

修正算法，只允许最多 $3n$ 次校正，如果还没有得到状态 $n$，那么就认为很有可能到达了状态 $0$，而非状态 $n$，抛弃当前的赋值，重新生成一个继续循环。算法伪代码如下：

可以算得，随机赋值经过 $3n$ 步修正得到正确解 $S$ 的概率 $q \ge \frac{c}{\sqrt{n}}(\frac{3}{4})^n$，这样平均重复 $\frac{1}{q}$ 次才能得到正确解，重复 $\frac{2}{q}$ 次得到正确解的概率大于 $\frac{1}{2}$，由概率放大过程可知，重复 $2k/q$ 次得到正确解的概率大于 $1-1/2^k$。

对 $q$ 的证明过程比较复杂，一般人很难想到，可以查阅《概率与计算》。如果考试要证明这种概率，可以直接略过，先试着假设 $q$ 是一个常数，得到结论之后，仔细来计算这个 $q$，放缩真的是一门艺术，需要仔细斟酌。

因此，总的时间复杂度为 $O(2k\frac{1}{c}n^{1/2}(\frac{4}{3})^n) \times m$。

MAX-SAT 随机算法

Random-Sample 算法

Random-Sample 算法是一种随机抽样算法。

我们来分析最开始推出的这个最最最 Naive 的算法：

定义随机变量 $Y_i$：

$Y_i = \begin{cases} 1, 子句 C_i 被满足 \\ 0, 子句 C_i 未被满足 \end{cases}$

$\begin{aligned} & P(C_i 未被满足) = \left(\frac{1}{2}\right)^{|C_i|} \le \frac{1}{2} \\ & P(C_i 被满足) = 1- P(C_i 未被满足) \ge \frac{1}{2} \end{aligned}$

因此可以求得 $Y_i$ 的均值：

$E(Y_i) \ge \frac{1}{2}$

定义随机变量 $Y$ 为被满足的子句总个数：

$E(Y) = \sum_{i=1}^mE(Y_i) \ge \frac{m}{2}$

令 $opt$ 为优化解满足的子句个数，我们得到：

$\frac{opt}{E(Y)} \le \frac{m}{E(Y)} \le 2$

也就是说，Random-Sample 得到的变量赋值能够满足的析取子句的个数不少于优化解的 $\frac{1}{2}$，我们称这个算法为 $E(2)$-近似算法。

Random-Round 算法

Random-Round 算法是一种随机舍入算法。

算法过程如下：

第 5 行可以这样理解：整数规划问题的最优解（虽然无法直接求得，但是可以穷举）一定不优于线性规划问题的最优解，因为取值范围更小。整个算法中最关键的是表示成 0-1 规划问题。

定随机变量义 $x_i, y_j$:

$x_i = \begin{cases} 1, 第 i 个变量取真 \\ 0, 第 i 个变量取假 \end{cases}$

$y_j = \begin{cases} 1, 子句 C_j 被满足 \\ 0, 子句 C_j 未被满足 \end{cases}$

MAX-SAT 表示成 0-1 规划问题，就是要：

1. 最大化满足的子句个数

   $\max y_1 + y_2 + \cdots + y_m$

2. 将子句满足与否用数学式子表示

   $s.t. \sum_{i\in C_j^+} x_j + \sum_{i\in C_j^-}(1-x_j) \ge y_j, \quad 1 \le j \le m$

3. 值域要求

   $x_i \in \{0, 1\}, \quad 1 \le i \le n$

   $y_j \in \{0, 1\}, \quad 1 \le j \le m$

松弛 0-1 规划问题的约束条件可以得到线性规划问题，就是将 $x_i$ 和 $y_j$ 的值域范围从原来的两个值 $\{0, 1\}$ 变为 区间$[0, 1]$。

原理既然理解了，那么怎么证明算法的效果比较好呢（$E(1.6)$-近似算法）？同样是进行一系列数学运算。

时间复杂度主要花在了调用线性规划求解算法上，是多项式时间的。

同 Random-Sample 的证明思路一样，我们首先要计算 $P(C_j 被满足)$，这里先不分析，直接给出结论：

引理：$P(C_j 被满足) \ge (1-1/e)y_j^*$。

那么，同样计算一下满足子句总数 $Y$ 的期望：

$E(Y) = \sum_{i=1}^mE(Y_j) \ge \sum_{j=1}^m (1-1/e)y_j^*$

$\frac{opt}{E(Y)} \le \frac{y_1*+\cdots+y_m*}{E(Y)} \le \frac{e}{e-1} \approx 1.6$

结论：Random-Round 算法是一个多项式时间的 $E[e/(e-1)]$-近似算法。

下面证明引理。$C_j$ 不被满足等价于：所有不取非的变量（$C_j^+$）取了 $0$，且所有取非的变量（$C_j^-$）取了 $1$。又因为返回的结果中 $x^*$ 取 $0$ 和 $1$ 的概率分别为 $1-x^*$ 和 $x^*$。

$\begin{aligned} P(C_j不被满足) &= \prod_{i \in C_i^+}(1-x_i^*)\prod_{i \in C_i^-}x_i^* \\ &= \left( \left( \prod_{i \in C_i^+}(1-x_i^*)\prod_{i \in C_i^-}x_i^* \right)^{1/|C_j|} \right)^{|C_j|} \\ &\le \left( \frac{\sum_{i \in C_i^+}(1-x_i^*)\sum_{i \in C_i^-}x_i^*}{|C_j|} \right)^{|C_j|} \\ &= \left(1- \frac{\sum_{i \in C_i^+}x_i^*\sum_{i \in C_i^-}(1-x_i^*)}{|C_j|} \right)^{|C_j|} \\ &\le \left( 1-\frac{y_j^*}{|C_j|} \right)^{|C_j|} \end{aligned}$

因此：

$P(C_j 被满足) \ge 1-\left( 1-\frac{y_j^*}{|C_j|} \right)^{|C_j|}$

再利用一个引理：

$1-(1-r/k)^k \ge [1-(1-1/k)^k]r$ 对 $r\in[0, 1]$ 和整数 $k$ 成立。

左端函数对 $r$ 求二阶导，验证是上凸函数，右端函数是线性函数，验证两个端点（0, 1）即可。

得到：

$\begin{aligned} P(C_j 被满足) &\ge 1-\left( 1-\frac{y_j^*}{|C_j|} \right)^{|C_j|} \\ & \ge \left[ 1- (1-1/|C_j|)^{|C_j|} \right] y_j^* \\ &\ge (1-1/e)y^*_j \end{aligned}$

在随机算法中，经常会用到这个不等式：$(1+a)^b \approx e^{ab}$ 或者 $(1+a)^b \le e^{ab}$。
参考这篇文章：

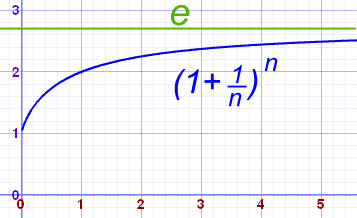
证明过程参考 Quora 上的回答。

Random-Mix 算法

Random-Mix 算法是一个混合随机算法。

算法伪代码如下：

假设赋值 $C$ 满足的子句个数为随机变量 $Z$，有：

$\begin{aligned} E(Z) &\ge \frac{1}{2}E(X+Y) \\ &= \sum_{i=1}^mE(X_i) + \sum_{i=1}^mE(Y_i) \\ &= \sum_{i=1}^m\left[ E(X_i) + E(Y_i) \right] \\ \end{aligned}$

又因为：

$E(X_i) = 1\cdot P(C_i=1) = 1 - \frac{1}{2^{|C_i|}} \ge \left( 1 - \frac{1}{2^{|C_i|}} \right) y_i^*$

前面已经得到：

$E(Y_i) \ge \left[ 1- (1-1/|C_j|)^{|C_j|} \right] y_i^*$

因此：

$\begin{aligned} E(X_i) + E(Y_i) &\ge \left( 1 - \frac{1}{2^{|C_i|}} \right) y_i^* + \left[ 1- (1-1/|C_i|)^{|C_i|} \right] y_i^* \\ &= \left\{ \left( 1 - \frac{1}{2^{|C_i|}} \right) + \left[ 1- (1-1/|C_i|)^{|C_i|} \right] \right\}y_i^* \\ &\ge \frac{3}{2}y_i^* \end{aligned}$

其中那一长串 $\ge \frac{3}{2}$ 可以通过求导证明。

最终得到：

$\frac{opt}{E(Z)} \le \frac{4}{3}$

也就是说 Random-Mix 是一个多项式时间的 $E(4/3)$-近似算法。

去随机化

前面的三种随机算法，都是在平均情况下，可以达到相应的近似比，我们希望消除其随机性，得到一个确定性的算法，使之不管在什么情况下，都能达到某个近似比。

把算法对 $x_1, \cdots, x_n$ 依次赋值的过程看作是一棵树，第 $i$ 层的结点表示 $x_1, \cdots, x_i$ 已经被赋值，给每个节点 $u$ 赋予一个属性 $g(u) = E(\#|x_1, \cdots, x_i)$，即 $x_1, \cdots, x_i$ 已经确定后，被满足的子句个数的期望值。如下图所示：

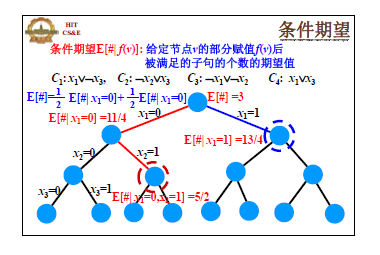
结论：任意节点的条件期望可以在多项式时间内被计算。比如给定了 $x_1=0$，那么 $C_1$ 为真的概率就知道了，再综合析取式，总的满足的析取式数量的期望就可以算出来。这个结论很重要，集合平衡配置问题之所以不能直接去随机化，就是因为条件期望的计算不是多项式时间的。

DetAssign 算法

改进 Random-Sample 算法，每次不是随机选取，而是选择均值更大的赋值方案。DetAssign 是近似比为 $2$ 的多项式时间确定性算法。

假设结点 $u$ 的儿子结点为 $v$（选择文字赋值 $0$）和 $w$（选择文字赋值 $1$），则有：

$g(u) = \frac{1}{2}g(v) + \frac{1}{2}g(w)$

根据期望论证，必有 $g(u) \ge g(v)$ 或者 $g(u) \ge g(w)$。我们每次做赋值选择的时候，选择较大的那一个赋值的话，就可以得到：

$\begin{aligned} Random-Sample 算法的平均情况 &= E(\#) \\ &\le g(u_0) \le g(u_1) \cdots \le g(u_n) \\ &= DetAssign 算法返回的 x_1, \cdots, x_n 赋值满足的子句个数 sat \end{aligned}$

因为 $\frac{opt}{E(\#)} \le 2$，所以 $\frac{opt}{sat} \le 2$。

DetRound 算法

改进 Random-Round 算法，每次不是随机舍入，而是选择均值更大的舍入方案。DetRound 是近似比为 $e/(e-1)$ 的多项式时间确定性算法。

与上面的证明类似，这次：

$g(u) = g(v)(1-x_i^*) + g(w)x_i^*$

同样有 $g(u) \ge g(v)$ 或者 $g(u) \ge g(w)$。之后的证明过程和上面一模一样。得到 $\frac{opt}{sat} \le e(e-1)$。

DetMix 算法

综合 DetAssign 和 DetRound，选择更优的结果。DetMix 是近似比为 $4/3$ 的多项式时间确定性算法。

DNF 满足性赋值随机算法

DNF 是析取范式，要求一个合取子句满足即可，我们要求解的是能够使 $D_1, \cdots, D_m$ 之一被满足的可行的对 $x_1, \cdots, x_n$ 的赋值个数 $c(F)$。

朴素算法

对所有的赋值方案进行 $N$ 次抽取，算得其中有 $X$ 次满足，对满足比的估计为 $X/N \approx c(F)/2^n$。由于比较简单，这里就不再写伪代码了。

这里用到了切尔诺夫界的知识。为了得到 $(\epsilon, \delta)$ 近似（错误率超过 $\epsilon$ 的概率不超过 $\delta$），我们构造如下：

$P[|X/N - c(F)/2^n| > \epsilon c(F)/2^n] \le \delta \\$

用 $X_i=1$ 表示第 $i$ 次抽样的随机样本满足某个合取式，由于 $\mu = E(X/N) =E(X)/N=\sum_{i=1}^NE(X_i)/N=c(F)/2^n$，所以：

$P[|X/N - \mu| > \epsilon \mu] \le 2\exp{-\frac{\mu \epsilon^2}{3}} \le \delta$

解得：

$\begin{aligned} \mu &\ge -3\ln \frac{\delta}{2} \end{aligned}$

得到的这个结果因为不包含抽样大小 $N$，所以并没有什么用，我们可以换一个方式计算 $\mu' = E(X) = Nc(F)/2^n$。再利用 Chernoff 界：

$P[X-\mu'>\epsilon \mu'] \le 2 \exp{-\frac{\mu' \epsilon^2}{3}} \le \delta$

解得：

$\begin{aligned} \mu' &\ge -\frac{3}{\epsilon^2}\ln \frac{\delta}{2} \\ N &\ge 3\cdot 2^n\ln(2/\delta)/\epsilon^2 c(F) \end{aligned}$

Buboly-Karp 算法

朴素抽样次数要求太大，因为目标样本在样本空间内非常稀疏，需要很多次抽样才能找到一个目标样本。老师上课时举了一个很生动的例子，问什么估计 $\Pi$ 的值时，要选正方形的内切圆，而不是随意取一个很小很小的圆，就是这个道理。

我们需要改造样本空间，去掉不能使单个合取式 $D_j$ 满足的样本。

对于第 $i$ 个子句，令 $SC_i=\{a|赋值a满足 D_i\}$，比如对于 $D_i=\lnot x_1\land x_3$，只有 $x_1=0, x_3=1$ 并且其他变量任意的赋值满足，因此 $|SC_i|=2^{n-|C_i|}$。

总的样本空间 $U$ 变小了：

$|U| = \sum_{i=1}^m |SC_m|$

总样本空间里面去除重复赋值的总共可满足个数为 $c(F) = |\cup_{i=1}^mSC_i|$。

抽样估计的是不重复率 $c(F)/|U|$，为了实现 $|U|$ 上的均匀抽样，需要以 $|SC_i|/|U|$ 的概率从 $|SC_i|$ 中抽取。这样，抽中任何一个 $|SC_i|$ 中的赋值 $(i, a)$ 的概率为：

$\begin{aligned} P[取中 (i, a)] &= P(在 SC_i 中抽取) P(取中 (i, a)|在 SC_i 中抽取) \\ &= |SC_i|/|U| \cdots \frac{1}{|SC_i|} \\ &= \frac{1}{|U|} \end{aligned}$

证明了均匀性，后续证明过程就与前面差不多了，最后会得到 $3\cdot |U|\ln(2/\delta)/\epsilon^2 c(F)$

集合平衡配置问题

一共有 $m$ 个实验对象，每个对象有 $n$ 个特征（取值为 $0,1$ 表示是否具有这个特征），需要将这些实验对象分为两组，要求每个特征在第一组和第二组中的出现的对象总数相差尽可能少。

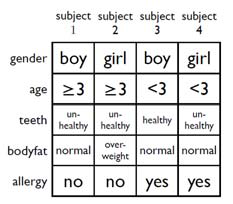
输入一个 $n\times m$ 的矩阵 $A$，用向量 $X_{m \times 1}$ 表示分配方案，$x_i \in \{-1, 1\}$ 表示第 $i$ 个对象被分配的组。我们的到下面的等式：

$\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm} \end{pmatrix}_{n\times m} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \end{pmatrix}_{m \times 1} = \begin{pmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{pmatrix}_{n \times 1}$

其中 $c_i$ 表示特征 $i$ 在组 $1$ 和组 $-1$ 相差的数目。为了尽量平衡，我们应该让最大的 $c_i$ 取值最小。即最小化 $|C|_\infty$。

解决这个问题，用随机算法，最最最 Naive 的想法就是 $X$ 向量中每个元素的分配随机选择 $1$ 或者 $-1$，根本不考虑特征的分布情况。我们接下来就证明这种算法的效果好不好。

先给出结论：对于任意的 0-1 矩阵 $A_{n\times m}$ 和任意选取的分配方案 $X_{m \times 1}$，有：

$P[|C|_\infty \ge \sqrt{12m\ln n}] < \frac{2}{n}$

证明过程如下。

$\begin{aligned} P(|C|_\infty > t) &= P\left(\cup_{i=1}^n\left|\sum_{j=1}^{m}a_{ij}x_j\right| > t\right) \\ & \le \sum_{i=1}^n P\left(\left|\sum_{j=1}^{m}a_{ij}x_j\right| > t\right) \tag{1} \end{aligned}$

下面关键是对 $P\left(\left|\sum_{j=1}^{m}a_{ij}x_j\right| > t\right)$ 进行放缩求一个上界出来。这里就可以用到 Chernoff 界了。

总共有 $m$ 次分配，随机变量 $Y_j$ 表示对特征 $i$ 的第 $j$ 次分配的结果，如果 $x_j=1$，则 $Y_j=1$，如果 $x_j=-1$，则 $Y_j=0$。

$Y_j = \begin{cases} 1, \quad P(Y_j=1)=\frac{1}{2} \\ 0, \quad P(Y_j=0)=\frac{1}{2} \end{cases}$

计算均值得到 $\mu = E(Y) = \sum_{j=1}^m E(Y_j) = \frac{m}{2}$。

因为 $a_{ij}$ 中不是全 $1$（$0$ 表示特征不出现），所以满足不等式（$a_{ij}$ 对所有 $j$ 全 $1$ 时取等号）：

$\begin{aligned} P\left(\left|\sum_{j=1}^{m}a_{ij}x_j\right| > t\right) &\le P\left[\left(Y<\frac{m}{2}-\frac{t}{2}\right) \lor \left(Y>\frac{m}{2}+\frac{t}{2}\right)\right] \\ &= P\left(|Y-\mu| > \frac{t}{2}\right) \\ &= P\left(|Y-\mu| > \delta \mu\right), \quad \delta=\frac{t}{m} \\ &\le 2\exp{-\frac{\mu \delta^2}{3}} \\ &= 2\exp{-\frac{t^2}{6m}}, \quad 取 t = \sqrt{12m\ln n} \\ &= \frac{2}{n^2} \end{aligned}$

将这个结果带入 $(1)$ 式中，就可以得到：

$P(|C|_\infty > \sqrt{12m\ln n}) \le n \times \frac{2}{n^2} = \frac{2}{n}$

去随机化

在前面的算法中，我们是随机的返回任意一个配置方案，只算了坏事件的概率上界，坏事件仍然可能发生，如何完全去除随机化呢？是否存在确定性算法，使得 $|C|_\infty < \sqrt{12m\ln n}$？

同前面 Random-Sample 和 Random-Round 算法的思想一样，首先定义条件概率并将方案的确定过程表达成树。

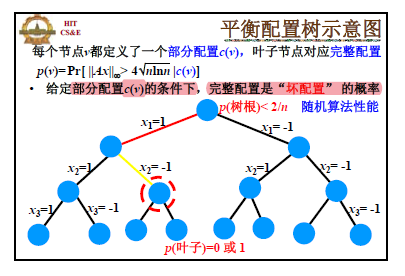
对结点 $u$ 和它的两个子节点 $v$ 和 $w$，我们有等式：

$p(u) = p(v)P(x_i=1) + p(w)P(x_i=0)$

根据期望论证，必然有 $p(u) \ge p(v)$ 或者 $p(u) \ge p(w)$ 成立。我们选择小概率的方向进行集合配置。最终叶子结点的概率要么是 $0$，要么是 $1$，我们得到的一定就是 $0$ 的那一个了。

但是这里不同于前面 Random-Sample 和 Random-Round 算法的是，$p$ 的计算并不能在多项式时间内完成，而是指数时间的。

解决办法是，定义 $p$ 的一个上界 $q$，那么 $q = 0 \Rightarrow p=0$。并且这个上界计算不会太复杂。

$\begin{aligned} q(u) &= \min \left( 1, \sum_{j}P\left[|C_j| > 4\sqrt{n \ln n} | c(u)\right] \right) \\ &\ge P\left[\lor_{j} \left( |C_j| > 4\sqrt{n \ln n} | c(u) \right)\right] \\ &= P\left[|C_j|_\infty > 4\sqrt{n \ln n} | c(u)\right] \\ &= p(u) \end{aligned}$

$q$ 满足三个性质：

1. $q(u) = 0 \Rightarrow p(u) = 0$

2. $q(叶子) = 0或1$，一旦具体的配置方案确定，要么满足 $|C|_\infty \ge 4\sqrt{n\ln n}$，要么不满足

3. $q(树根) \le 2/n$

   根据之前的结论可以得到。

我们看到，$q$ 相比于 $p$，从原来的求无穷范数超过某个值的概率，变为了单个值超过某个值的概率，计算会简化许多，可以在多项式时间内计算。

最大割问题

首先计算 $c_i \ge \frac{m}{2}$ 的概率，定义随机变量：

$Y_j = \begin{cases} 1, \quad 边 j 的两个顶点分别在 V 和 S_i -V 中, p = \frac{1}{2} \\ 0, \quad 边 j 的两个顶点同时在 V 和 S_i - V 中, p = \frac{1}{2} \end{cases}$

显然 $c_i = \sum_{j=1}^mY_j$，那么我们可以得到 $c_i = mE(Y_j) = \frac{m}{2}$。

那么这里如果直接用 Markov 不等式的话，得到这个结果：

$p(c_i \ge \frac{m}{2}) \le 1$

这个结论没有任何用，这里采用更加精细化的放缩（之所以可以这样做，是因为 $c_i$ 永远不超过 $m$）：

$\begin{aligned} \frac{m}{2} &= E(c_i) \\ &= \sum_{k}k\cdot P(c_i=k) \\ &= \sum_{k < m/2} k \cdot P(c_i < \frac{m}{2}) + \sum_{k \ge m/2} k \cdot P(c_i\ge \frac{m}{2}) \\ &\le (m/2-1)(1-p) + mp \end{aligned}$

解得 $p(c_i \ge \frac{m}{2}) \ge \frac{1}{m/2+1}$，也就是说，执行一遍循环得到 $c_i \ge \frac{m}{2}$ 的割的概率至少为 $\frac{1}{m/2+1}$，根据几何分布的期望，算法平均最多执行 $\frac{m}{2}+1$ 次循环就可以得到一个 $c_i \ge \frac{m}{2}$ 的割。

算法执行次数为随机变量 $X$，那么 $E(X) = \frac{m}{2}+1$，利用 Markov 不等式得到：

$\begin{aligned} P[X \ge 2E(X)] &\le \frac{1}{2} \\ P[X \ge m+2] &\le \frac{1}{2} \\ \end{aligned}$

也就是说：算法执行 $m+1$ 遍才得到（或者说『还没有得到』）一个 $c_i \ge \frac{m}{2}$ 的概率不超过 $\frac{1}{2}$。

参考资料

1. 《概率与计算》
2. 《随机算法》

附录