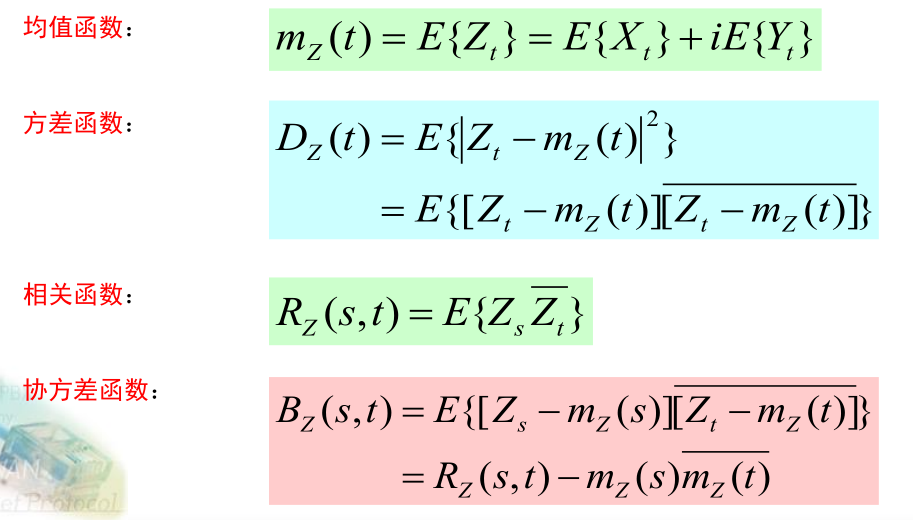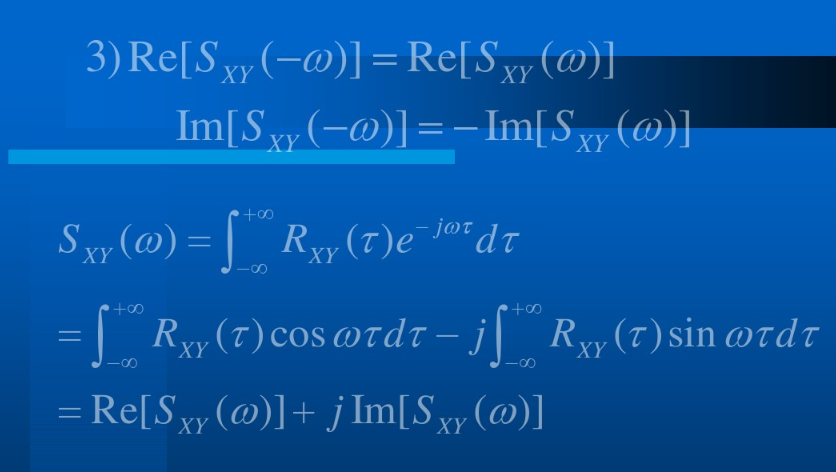傅里叶变换、{能量,功率,互}谱密度、白噪声随机过程

一篇文章详细搞懂傅里叶变换的数学推导及其本质、应用等等。

傅里叶变换

19 世纪早期，Joseph Fourier 发现任何周期函数可以表示为正余弦函数的级数和。这就是傅里叶级数。

变换过程如下图所示：

fourier-transform

傅里叶级数

傅里叶级数有两种形式，分别是三角形式（Trigonometric）和指数形式（Exponential），表示如下：

$\begin{aligned} x\left( t \right) &= a_0 + \sum\limits_{n = 1}^\infty {\left( {a_n \cos \left( {n\omega _0 t} \right) + b_n \sin \left( {n\omega _0 t} \right)} \right)} \quad \quad Trigonometric \cr &= \sum\limits_{n = - \infty }^\infty {c_n e^{jn\omega _0 t} } \quad \quad Exponential \end{aligned}$

我们将在后面证明两者的等价性。

现在首先证明三角形式的傅里叶级数展开是正确的，证明过程分为三步：

证明偶周期函数的傅里叶级数展开式
证明奇周期函数的傅里叶级数展开式
证明任意周期函数的傅里叶级数展开式

偶周期函数的傅里叶级数展开式

偶周期函数 $x_e(t)$ ：

$x_e (t) = \sum\limits_{n = 0}^\infty {a_n \cos \left( {n\omega _0 t} \right)}$

因为当 $n = 0$ 时， $\cos(n\omega t) = 1$ ，所以通常也会写为：

$x_e (t) = a_0 + \sum\limits_{n = 1}^\infty {a_n \cos \left( {n\omega _0 t} \right)}$

这个过程可以理解为『生成』过程，通过叠加一系列周期不同的波，赋予不同的系数 $a_n$ ，最终形成了我们想要的偶周期函数 $x_e(t)$ 。

$a_0$ 就是 $x_e(t)$ 一个周期内的平均值，下面将会证明。

证明上面的式子的正确性，就是要证明 $a_n$ 的存在性，那么我们一个一个解出这些 $a_n$ 和 $b_n$ 即可。

左右两边同乘 $\cos ( {m\omega _0 t})$ ，便于后续利用正交性质：

$x_e (t)\cos \left( {m\omega _0 t} \right) = \sum\limits_{n = 0}^\infty {a_n \cos \left( {n\omega _0 t} \right)} \cos \left( {m\omega _0 t} \right)$

对一个周期进行积分：

$\int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} = \int\limits_T {\sum\limits_{n = 0}^\infty {a_n \cos \left( {n\omega _0 t} \right)} \cos \left( {m\omega _0 t} \right)dt}$

积分号移到求和号内部，同时利用 $\cos a\cos b = \frac{1}{2}\left[\cos(a+b) + \cos(a-b)\right]$ 积化和差：

$\begin{aligned} \int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} &= \sum\limits_{n = 0}^\infty {a_n \int\limits_T {\cos \left( {n\omega _0 t} \right)\cos \left( {m\omega _0 t} \right)dt} } \\ & = \sum\limits_{n = 0}^\infty {a_n \int\limits_T { {1 \over 2}\left( {\cos \left( {\left( {m + n} \right)\omega _0 t} \right) + \cos \left( {\left( {m - n} \right)\omega _0 t} \right)} \right)dt} } \\ & = {1 \over 2}\sum\limits_{n = 0}^\infty {a_n \int\limits_T {\left( {\cos \left( {\left( {n + m} \right)\omega _0 t} \right) + \cos \left( {\left( {m - n} \right)\omega _0 t} \right)} \right)dt} } \end{aligned}$

将和的积分转为积分的和，同时利用余弦函数一个周期之内的积分为 0，对于 $\cos \left( {\left( {n+m} \right)\omega _0 t}\right)$ ，它的周期为 $\frac{T}{n+m}$ ，所以在 $T$ 内经过了 $(n+m)$ 个周期，积分一定为 0。

$\begin{aligned} \int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} &= \frac{1} {2}\sum\limits_{n = 0}^\infty {a_n \int\limits_T {\left( {\cos \left( {\left( {n + m} \right)\omega _0 t} \right) + \cos \left( {\left( {m - n} \right)\omega _0 t} \right)} \right)dt} } \\ & = \frac{1} {2}\sum\limits_{n = 0}^\infty {a_n \left( {\int\limits_T {\cos \left( {\left( {n + m} \right)\omega _0 t} \right)dt} + \int\limits_T {\cos \left( {\left( {m - n} \right)\omega _0 t} \right)dt} } \right)} \\ & = \frac{1} {2}\sum\limits_{n = 0}^\infty {a_n \int\limits_T {\cos \left( {\left( {m - n} \right)\omega _0 t} \right)dt} } \end{aligned}$

$\cos \left( {\left( {m - n} \right)\omega _0 t} \right)$ 的取值则需要根据 $m, n$ 的差值来确定：

$\begin{aligned} \int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} &= {1 \over 2}\sum\limits_{n = 0}^\infty {a_n \int\limits_T {\cos \left( {\left( {m - n} \right)\omega _0 t} \right)dt} } \\ &= \begin{cases} \int_T0 \cdot dt = 0, m \neq n \\ \int_T1\cdot dt = T, m = n \end{cases} \end{aligned}$

回到之前的积分：

$\int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} = {1 \over 2}\sum\limits_{n = 0}^\infty {a_n \int\limits_T {\cos \left( {\left( {m - n} \right)\omega _0 t} \right)dt} }$

只有 $m=n$ 的时候，右边的式子才不为 0，这样我们得到：

$\int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} = {\frac{1}{2}}a_m T \\ a_m = {\frac{2}{T}}\int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} \\ a_n = {2 \over T}\int\limits_T {x_e (t)\cos \left( {n\omega _0 t} \right)dt}$

在最后一个式子中，简单地用 $n$ 替代了上一个式子的 $m$ ，最终就求出了所有的 $a_n$ 。

证明过程还没有结束，因为没有考虑到 $m = 0$ 的情况，如果 $m = 0$ ，上面的 $m+n$ 就不一定为大于等于 $1$ 的整数了（在 $n = 0$ 的时候），也就得不出正交条件。

下面单独考虑：

$\begin{aligned} \int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} &= \sum\limits_{n = 0}^\infty {a_n \int\limits_T {\cos \left( {n\omega _0 t} \right)\cos \left( {m\omega _0 t} \right)dt} } \cr \int\limits_T {x_e (t)\cos \left( {0 \cdot \omega _0 t} \right)dt} &= \sum\limits_{n = 0}^\infty {a_n \int\limits_T {\cos \left( {n\omega _0 t} \right)\cos \left( {0 \cdot \omega _0 t} \right)dt} } \quad \quad {\text{but }}\cos \left( {0 \cdot \omega _0 t} \right) &= 1 \cr \int\limits_T {x_e (t)dt} &= \sum\limits_{n = 0}^\infty {a_n \int\limits_T {\cos \left( {n\omega _0 t} \right)dt} } \cr \int\limits_T {x_e (t)dt} &= Ta_0 \end{aligned}$

这样就得到了 $a_0$ 其实就是函数的均值：

$a_0 = \frac{1} {T}\int\limits_T {x_e (t)dt} = {\text{average of x}}_e \left( t \right)$

奇周期函数的傅里叶级数展开式

奇周期函数 $x_o(t)$ ：

$x_o(t) = \sum_0^{\infty}b_n\sin(n\omega_0 t)x$

使用类似于上面的过程，容易证明：

$b_n = \frac2T\int\limits_T {x_o (t)\sin \left( {n\omega _0 t} \right)dt}$

任意周期函数的傅里叶级数展开式

对于任意周期函数 $x(t)$ ：

$x_o \left( t \right) = \frac{1} {2}\left[ {x\left( t \right) - x\left( { - t} \right)} \right] \\ x_e \left( t \right) = \frac{1} {2}\left[ {x\left( t \right) + x\left( { - t} \right)} \right] \\$

分别对 $x_o(t)$ 和 $x_e(t)$ 求解傅里叶级数，最后解出 $x(t)$ 即可：

$x(t) = x_o(t) + x_e(t)$

最终得到：

$x_T \left( t \right) = a_0 + \sum\limits_{n = 1}^\infty {\left( {a_n \cos \left( {n\omega _0 t} \right) + b_n \sin \left( {n\omega _0 t} \right)} \right)}$

其中：

$\begin{aligned} a_0 &= {1 \over T}\int\limits_T {x_T \left( t \right)dt} \; = \;average \\ a_n &= {2 \over T}\int\limits_T {x_T \left( t \right)\cos \left( {n\omega _0 t} \right)dt} ,\quad n \ne 0 \\ b_n &= {2 \over T}\int\limits_T {x_T \left( t \right)\sin \left( {n\omega _0 t} \right)dt} \cr\end{aligned}$

证明完了三角形式展开的正确性，我们下面证明其与指数形式的等价性。

三角形式级数与指数形式的等价性

要证明三角形式级数：

$x_T \left( t \right) = a_0 + \sum\limits_{n = 1}^\infty {\left( {a_n \cos \left( {n\omega _0 t} \right) + b_n \sin \left( {n\omega _0 t} \right)} \right)}$

与指数形式级数的等价性：

$x_T \left( t \right) = \sum\limits_{n = - \infty }^{ + \infty } {c_n e^{jn\omega _0 t} }$

就是要证明：

$a_0 + \sum\limits_{n = 1}^\infty {\left( {a_n \cos \left( {n\omega _0 t} \right) + b_n \sin \left( {n\omega _0 t} \right)} \right)} = \sum\limits_{n = - \infty }^{ + \infty } {c_n e^{jn\omega _0 t} }$

下文假设 $x_T$ 为实函数，那么 $a_n, b_n$ 都将是实数。首先考虑常数项：

$a_0 = c_0$

所以 $c_0$ 也是函数 $x_T$ 的均值。只考虑周期为 $T$ 的分量，有：

$a_1 \cos (\omega _0 t) + b_1 \sin (\omega _0 t) = c_{ - 1} e^{ - j\omega _0 t} + c_1 e^{ + j\omega _0 t}$

只考虑周期为 $\frac{T}{2}$ 的分量：

$a_2 \cos (2\omega _0 t) + b_2 \sin (2\omega _0 t) = c_{ - 2} e^{ - j2\omega _0 t} + c_2 e^{ + j2\omega _0 t}$

推广到普遍情况，有：

$a_n \cos (n\omega _0 t) + b_n \sin (n\omega _0 t) = c_{ - n} e^{ - jn\omega _0 t} + c_n e^{ + jn\omega _0 t}$

这里简单分析一下。根据欧拉公式 $e^{ - jn\omega _0 t}$ 和 $e^{ - jn\omega _0 t}$ 是共轭的，为了消去它们的虚部，显然 $c_{-n}$ 和 $c_n$ 也需要共轭才行。不妨令 $c_n = c_{n, r} + j\cdot c_{n,i}$ ，这样 $c_{-n} = c^*_{n} = c_{n,r} - j\cdot c_{n,i}$ ，这样我们将右边展开来和左边进行对比一下：

$\begin{aligned} a_n \cos (n\omega _0 t) + b_n \sin (n\omega _0 t) &= c_{ - n} e^{ - jn\omega _0 t} + c_n e^{ + jn\omega _0 t} \cr &= (c_{n,r} - jc_{n,i} )\left( {\cos \left( {n\omega _0 t} \right) - j\sin \left( {n\omega _0 t} \right)} \right) + (c_{n,r} + jc_{n,i} )\left( {\cos \left( {n\omega _0 t} \right) + j\sin \left( {n\omega _0 t} \right)} \right) \cr &= 2c_{n,r} \cos \left( {n\omega _0 t} \right) - 2c_{n,i} \sin \left( {n\omega _0 t} \right) + j\left( {\cos \left( {n\omega _0 t} \right)\left( {c_{n,r} - c_{n,r} } \right) + \sin \left( {n\omega _0 t} \right)\left( {c_{n,i} - c_{n,i} } \right)} \right) \cr &= 2c_{n,r} \cos \left( {n\omega _0 t} \right) - 2c_{n,i} \sin \left( {n\omega _0 t} \right) \cr\end{aligned}$

对比得到：

$a_n = 2c_{n,r} \\ b_n = -2c_{n,i} \\$

即：

$\begin{aligned} c_n &=\frac{a_n}2-j\frac{b_n}2, \ n \ne 0, \quad with \ c_{-n}=c_n^* \\ &= \frac{1}{T}\int_{T}x(t)\cos(n\omega_0t)dt - j\frac{1}{T}\int_{T}x(t)\sin(n\omega_0t)dt \\ &= \frac{1}{T}\int_Tx(t)e^{-jn\omega_0 t}dt \end{aligned}$

从傅里叶级数到傅里叶变换

对于周期函数 $x_T(t)=x_T(t+T)$ ，傅里叶级数展开为：

$x_T(t) = \mathcal{F}^{-1}[X[k]] = \sum_{k=-\infty}^{\infty}X[k]e^{jk\omega_0 t}$

这里的 $X[k]$ 相当于前文的 $c_n$ ，是傅里叶系数：

$X[k] = \mathcal{F}[x_T(t)] = \frac{1}{T}\int_T x_T(t)e^{-jk\omega_0 t}dt$

我们定义:

$X(k\omega_0) \equiv TX[k] = \int_T x_T(t)e^{-jk\omega_0 t}dt$

傅里叶级数展开形式就变成了：

$x_T(t) = \frac{1}{T}\sum_{k=-\infty}^{\infty}TX[k]e^{jk2\pi f_0t} = \frac{1}{2\pi}\sum_{k = -\infty}^{\infty}X(k\omega_0)e^{jk\omega_0t}\omega_0$

当 $X_T(t)$ 的周期 $T \to \infty$ 时，就变成了非周期函数。

两个频率分量之间的差值趋于 0：

$T \to \infty \implies \omega_0 = \frac{2\pi}{T} \to 0$

离散的频率趋于连续：

$k\omega_0 | {\omega_0 \to 0} \implies \omega$

作和变成了积分，这就是傅里叶逆变换：

$x(t) \equiv \lim_{t \to \infty}x_T(t) = \lim_{\omega_0 \to 0 }\frac{1}{2\pi} \sum_{k=-\infty}^{\infty}X(k\omega_0)e^{jk\omega_0 t}\omega_0 = \frac{1}{2\pi}\int_{-\infty}^{\infty}X(\omega)e^{j\omega t}d\omega$

其中用到了：

$\lim_{\Delta x\to 0}\sum_{k=-\infty}^{\infty}f(k\Delta x)\Delta x = \int_{-\infty}^{\infty}f(x)dx$

同时在 $T$ 内的积分变成了在整个时间轴上的积分：

$X(\omega) \equiv \lim_{T \to \infty} X(k\omega_0) = \lim_{T\to \infty} \int_{T} x_T(t)e^{-jk\omega_0t}dt = \int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt$

这就得到了前向傅里叶变换：

$X(\omega) = \int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt \quad or \quad X(f) = \int_{-\infty}^{\infty}x(t)e^{-j2\pi ft}dt$

逆傅里叶变换：

$x(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}X(\omega)e^{j\omega t}d\omega = \int_{-\infty}^{\infty}X(f)e^{j2\pi ft}df$

平稳过程的功率谱密度

信号可以分为能量型信号和功率型信号两大类。一般来说，周期信号和随机信号是功率信号，而非周期的确定信号是能量信号。能量型『能量有限』、『平均功率为 0』的信号，功率型信号是『能量无限』、『平均功率不为 0』的信号。

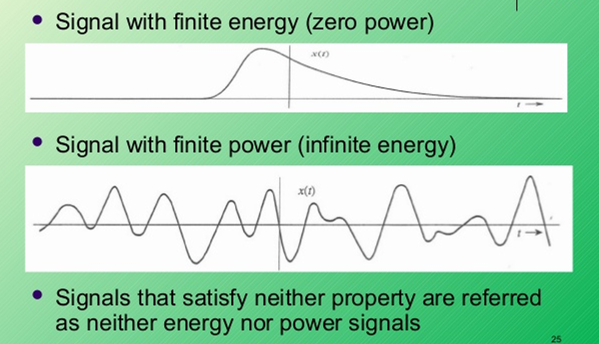
能量型信号

当且仅当信号在所有时间上的能量不为 0 且有限时，该信号为能量信号。典型的有方波信号、三角波信号等。对能量信号进行傅立叶分析可知其能量在频域的分布情况。

$W = \int_{-\infty}^{+\infty}f^2(t)dt < \infty$

其中 $f(t)$ 为信号， $W$ 为总能量。

傅里叶变换存在条件

回顾连续函数存在傅里叶变换的条件：

$f(t)$ 在任意区间上满足 Dirichlet 条件，即函数连续或只有有限个第一类间断点，且只有有限个极值点。
$f(t)$ 在 $(-\infty, +\infty)$ 上绝对可积

$\displaystyle \left\Vert\,f\,\right\Vert _1 \triangleq \int_{-\infty}^\infty \left\vert f(t)\right\vert dt < \infty$

可以记作 $f \in L_1$ ，即 $f$ 属于所有 $L_1$ 范数有限（ $||f||_1 < +\infty$ ）的信号组成的集合

另一种表达形式是用二范数：

$||f||_2^2 \triangleq \int_{-\infty}^{+\infty}|f(t)|^2dt < \infty$

可以记作 $f \in L_2$

更加推广，可以得到结论：只需 $f \in L_p, p \in [1, 2]$ 即可。

这是因为，很明显：

$\int_{-\infty}^{+\infty}|f(t)|^pdt < \infty \implies \int_{-\infty}^{+\infty}|f(t)|dt < \infty, p \in [1, 2]$

能量谱密度

在 $\int_{-\infty}^{+\infty}f^2(t)dt < \infty$ 或者 $\int_{-\infty}^{+\infty}|f(t)|dt < \infty$ 的情况下(2)，能量型信号 $f(t)$ 的傅里叶变换存在，即：

$F(\omega) = \int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt$

其逆变换为：

$f(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{j\omega t}d\omega$

$F(\omega)$ 称为信号 $f(t)$ 的频谱函数。频谱函数的模称为 $f(t)$ 的振幅频谱。

在傅里叶变换存在的条件下，函数满足 Parseval 等式：

$W = \int_{-\infty}^{+\infty}|f(t)|^2dt = \frac{1}{2\pi}\int_{-\infty}^{+\infty}|F(\omega)|^2d\omega = \int_{-\infty}^{+\infty}|F(2\pi\xi)|^2d\xi$

根据上式，定义能量型信号的能量谱密度为：

$E(\omega) = |F(\omega)|^2$

这样就有：

$W = \frac{1}{2\pi} \int_{-\infty}^{+\infty}E(\omega)d\omega$

这意味着，时域和频域的能量是守恒的。只是相差一个系数 $\frac{1}{2\pi}$ ，这个系数可以通过 $\xi = \frac{\omega}{2\pi}$ 消除。

傅里叶变换的另一种形式为：

${F}(\xi )=\int _{-\infty }^{+\infty }f(t)\ e^{-2\pi jt\xi }\,dt$

其逆变换为：

$f(t) = \int_{-\infty}^{+\infty}F(\xi)e^{2\pi j t \xi}d\xi$

不难得出：

$\int_{-\infty}^{+\infty}F(\xi)e^{2\pi j t \xi}d\xi = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{j\omega t}d\omega$

这样的话就不会再有系数 $\frac{1}{2\pi}$ ，前后两种傅里叶变换只是得到的傅里叶函数的自变量不同，本质上是一样的。

这其中用到的关键转换是：

$\xi = \frac{w}{2\pi}$

因此得到的两个傅里叶变换只是自变量不同罢了，本质上是等价的。

功率型信号

能量无限，功率有限的信号称为功率型信号。一般是周期性信号。

由于『能量无限』，不再满足绝对可积的条件。

但是其『功率有限』：

$P_f = \lim_{T \to \infty} \frac{1}{2T}\int_{-T}^{T}f^2(t)dt < \infty$

$P_f$ 为信号的平均功率。

为了能够利用傅里叶变换给出平均功率的谱表达式，构造截尾函数：

$f_T(t) = \begin{cases} f(t), |t| \le T \\ 0, |t| > T \end{cases}$

那么后续积分的时候只会算一个周期内的积分， $f_T(t)$ 满足绝对可积性质：

$F(\omega, T) = \int_{-\infty}^{\infty}f_T(t)e^{-j\omega t}dt = \int_{-T}^{T}f(t)e^{-j\omega t}dt$

之前对能量型定义的是能量，这里对功率型信号 $f_T(t)$ 定义平均功率：

$P_{f_T} = \int_{-\infty}^{+\infty}f^2_T(t)dt$

由 Parseval 等式：

$P_{f_T} = \int_{-\infty}^{+\infty}f_T^2(t)dt = \frac{1}{2\pi}\int_{-\infty}^{+\infty}|F(\omega, T)|^2d\omega$

两边同时除以 $2T$ ，并由截尾函数的定义得到：

$\frac{1}{2T}\int_{-T}^{T}f^2(t)dt = \frac{1}{4\pi T}\int_{-\infty}^{+\infty}|F(\omega, T)|^2d\omega$

令 $T$ 趋于无穷，功率型信号 $f(t)$ 在 $(-\infty, +\infty)$ 上的平均功率可表示为：

$\begin{aligned} P_f &= \lim_{T \to \infty}\frac{1}{2T}\int_{-T}^{T}f^2(t)dt \\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} \lim_{T \to \infty} \frac{1}{2T}|F(\omega, T)|^2d\omega \end{aligned}$

功率型信号的平均功率谱密度，简称功率谱密度，被定义为：

$S(\omega) = \lim_{T \to \infty} E\left\{\frac{1}{2T}|F(\omega, T)|^2\right\}$

为什么需要取平均：不理解，问一下老师。

这样 $P_f$ 就可以表示为：

$P_f = \frac{1}{2\pi}\int_{-\infty}^{+\infty}S(\omega)d\omega$

令 $\hat{x}(\omega) = \frac{1}{\sqrt{2\pi}}F(\omega, T)$

$\mathbf {E} \left[\left|{\hat {x}}(\omega )\right|^{2}\right]=\mathbf {E} \left[{\frac {1}{T}}\int _{0}^{T}x^{*}(t)e^{i\omega t}\,dt\int _{0}^{T}x(t')e^{-i\omega t'}\,dt'\right]={\frac {1}{T}}\int _{0}^{T}\int _{0}^{T}\mathbf {E} \left[x^{*}(t)x(t')\right]e^{i\omega (t-t')}\,dt\,dt'.$

$S(\omega)$ 为双边功率谱密度，但在实际应用中，负频率不存在，故引入：

$G(\omega) = \begin{cases} 2S(\omega), \omega \ge 0 \\ 0, \omega < 0 \end{cases}$

平稳随机过程的样本函数是功率型的，以上公式对平稳过程均适用。

谱密度与自相关函数

维纳-辛钦（Wiener-Khintchine ）公式

平稳随机过程（必须呀！WSS，宽平稳随机过程也可以）的功率谱密度是他自相关函数的傅里叶变换。

自相关函数

自相关函数是时滞（time lag）的函数：

$R(\tau) = R_{xx}(\tau )=\operatorname {E} {\big [}\,x^*(t)x(t + \tau)\,{\big ]} = \operatorname {E} {\big [}\,x^*(t-\tau )x(t)\,{\big ]}\$

取共轭的是下标更小的那个，自相关、互相关都是这样的

注意：这里右边虽然有 $t$ ，但是结果与 $t$ 是无关的，这就是平稳过程的特性。

满足：

$R_{f}(-\tau )=R_{f}^{*}(\tau )$

白噪声的自相关函数为 $δ$ 函数：

$R_{nn}={E} \{n(t)n(t-\tau )\}=\delta (\tau )$

互相关函数：

$(f\star g)(\tau )\ {\stackrel {\mathrm {def} }{=}}\int _{-\infty }^{\infty }f^{*}(t)\ g(t+\tau )\,dt} {\displaystyle (f\star g)(\tau )\ {\stackrel {\mathrm {def} }{=}}\int _{-\infty }^{\infty }f^{*}(t)\ g(t+\tau )\,dt$

$R_{XY}(\tau )=\operatorname {E} \left[X^*_{t}Y_{t+\tau }\right]$

下标到底是前面大，还是后面大？哪个变量取共轭？

维基百科倾向于前面取共轭：

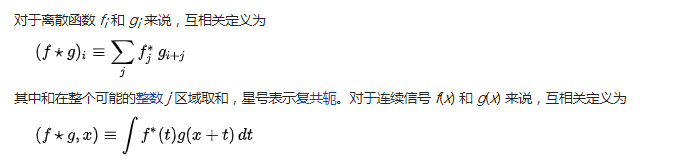
其他资料倾向于后面取共轭：

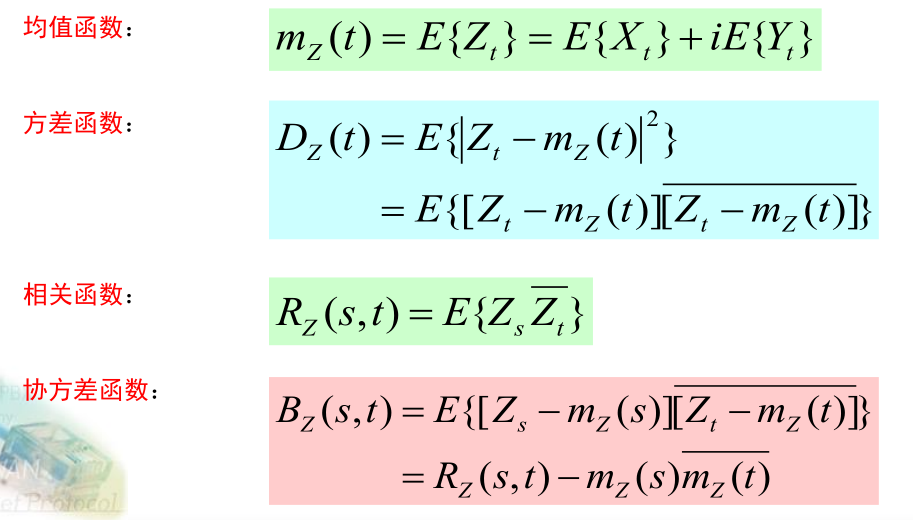
数学形式

如下：

$S(\omega) = \int_{-\infty}^{+\infty}R(\tau)e^{-j\omega\tau}d\tau$

$R(\tau) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}S(\omega)e^{j\omega t}d\omega$

另外，也有用圈频率的表达形式：

$\begin{aligned} S_X(f)=\mathcal{F} \{R_X(\tau) \}= \int_{-\infty}^{\infty} R_X(\tau) e^{-2 j \pi f \tau} \; d\tau, \end{aligned}$

$\begin{aligned} R_X(\tau)=\mathcal{F}^{-1} \{S_X(f)\}= \int_{-\infty}^{\infty} S_X(f) e^{2 j \pi f \tau} \; df. \end{aligned}$

例子：

证明

如下：

$\begin{aligned} S(\omega) &= \lim_{T \to \infty} E\left\{\frac{1}{2T}|F(\omega, T)|^2\right\} \\ &= \lim_{T \to \infty} \frac{1}{2T}E\left\{\int_{-T}^{T}f(t_1)e^{-j\omega t_1}dt_1 \int_{-T}^{T}f(t_2)e^{-j\omega t_2}dt_2\right\} \\ &= \lim_{T \to \infty} \frac{1}{2T}\int_{-T}^{T}\int_{-T}^{T}E[f(t_1)f(t_2)]e^{-j \omega (t_1 - t_2)}dt_1dt_2 \\ &= \lim_{T \to \infty} \frac{1}{2T}\int_{-T}^{T}\int_{-T}^{T}R(t_1 - t_2) e^{-j \omega (t_1 - t_2)} dt_1dt_2 \\ &\xlongequal{\tau = t_1 - t_2} \lim_{T \to \infty} \frac{1}{2T}\int_{-2T}^{2T}(2T - |\tau|)R(\tau)e^{-j\omega\tau} d\tau \\ &= \lim_{T \to \infty} \int_{-2T}^{2T}R(\tau)e^{-j\omega\tau} d\tau - \lim_{T \to \infty} \int_{-2T}^{2T}\frac{|\tau|}{2T}R(\tau)e^{-j\omega\tau} d\tau \\ \end{aligned}$

在 $\int_{-\infty}^{+\infty} |R(\tau)|d\tau < \infty$ 的情况下，上式中第二项为 0，此时可以得到：

$S(\omega) = \lim_{T \to \infty} \int_{-\infty}^{+\infty}R(\tau)e^{-j\omega \tau}d\tau$

也就是说，平稳随机过程在自相关函数绝对可积的情况下，维纳-辛钦公式成立。

功率谱密度的第二种定义：自相关函数的傅里叶变换。

根据逆变换：

$R(\tau) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}S(\omega)e^{j\omega \tau}d\omega$

令 $\tau = 0$ ，可以得到：

$R(0) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}S(\omega)d\omega = E[X^2(t)]$

也就是说，功率谱密度的积分是时滞为 0 时自相关函数的取值。

性质

实偶性质

$X(t)$ 是实平稳的，则自相关函数也是实偶函数，功率谱密度也是实偶函数。

$S^*(\omega) = \int_{-\infty}^{+\infty}R^*(\tau)e^{-j\omega\tau} = \int_{-\infty}^{+\infty}R(\tau)e^{-j\omega\tau} = S(\omega), 实函数 \\ S(-\omega) = \int_{-\infty}^{+\infty}R(-\tau)e^{-j\omega\tau} = \int_{-\infty}^{+\infty}R(\tau)e^{-j\omega\tau} = S(\omega), 偶函数$

等价形式

如下：

$S(\omega) = 2\int_{0}^{\infty}R(\tau)\cos(\omega\tau)d\tau \\ R(\tau) = \frac{1}{\pi}\int_0^{+\infty}S(\omega)\cos(\omega\tau)d\omega$

互谱密度

定义如下：

$S_{XY}(\omega) = \lim_{T \to \infty} \frac{1}{2T}E\left\{F_X(\omega, T)F_Y(\omega, T)\right\}$

维纳-辛钦定理：

$S_{XY}(\omega) = \int_{-\infty}^{+\infty}R_{XY}(\tau)e^{-j\omega \tau}d\tau \\ R_{XY}(\tau) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}S_{XY}(\omega)e^{j\omega \tau}d\omega$

圈频率形式：

$\begin{aligned} S_{XY}(f)=\mathcal{F} \{R_{XY}(\tau) \}= \int_{-\infty}^{\infty} R_{XY}(\tau) e^{-2 j \pi f \tau} \; d\tau. \end{aligned}$

当 $\tau = 0$ ：

$R_{XY}(0) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}S_{XY}(\omega)d\omega = E[X(t)Y(t)]$

这就是互谱密度的物理意义：其积分表示时滞为 0 时互相关函数的大小。

上式右边 $X(t), Y(t)$ 如果分别表示一个两端电压和流经该器件的电流，左边就是消耗的功率

功率谱密度的性质

正交过程： $X(t), Y(t)$ 满足：

$R_{XY}(\tau) = 0, S_{XY}(\omega) = 0$

此时有：

$R_{X+Y}(\tau) = R_{X}(\tau) + R_Y(\tau) \\ S_{X+Y}(\tau) = S_X(\omega) + S_Y(\omega)$

性质：

$S_{XY}(\omega) = S^*_{YX}(\omega) = S_{YX}(-\omega) \\ S_{XY}(\omega)|^2 \le S_X(\omega)S_Y(\omega)\\ Re[S_{XY}(-\omega)] = Re[S_{XY}(\omega)], 实部是偶函数 \\ Im[S_{XY}(-\omega)] = Im[S_{XY}(\omega)], 虚部是奇函数$

证明 1：

首先有：

$R^*_{YX}(\tau) = R_{XY}(-\tau)$

这是因为：

$R_{YX}^*(\tau) = \int\int x(t)y(t+\tau)f(x, t; y, t+\tau)dxdy$

$R_{XY}$

$\begin{aligned} S_{XY}(\omega) &= \int_{-\infty}^{+\infty}R_{XY}(\tau)e^{-j\omega\tau}d\tau \\ &\xlongequal{\text{let }\lambda = -\tau} \int_{-\infty}^{+\infty}R_{YX}^*(\lambda)e^{j\omega\lambda}d\lambda \\ &= S_{YX}^*(\omega )（注意这里是共轭，对应上面的指数不是 -j而是 j） \end{aligned}$

另外：

$\begin{aligned} S_{XY}(\omega) &= \int_{-\infty}^{+\infty}R_{XY}(\tau)e^{-j\omega\tau}d\tau \\ &\xlongequal{多取一个共轭} \int_{-\infty}^{+\infty}R_{YX}(\lambda)e^{-j(-\omega)\lambda}d\lambda \\ &= S_{XY}(-\omega ) \end{aligned}$

证明 2：

证明 3：

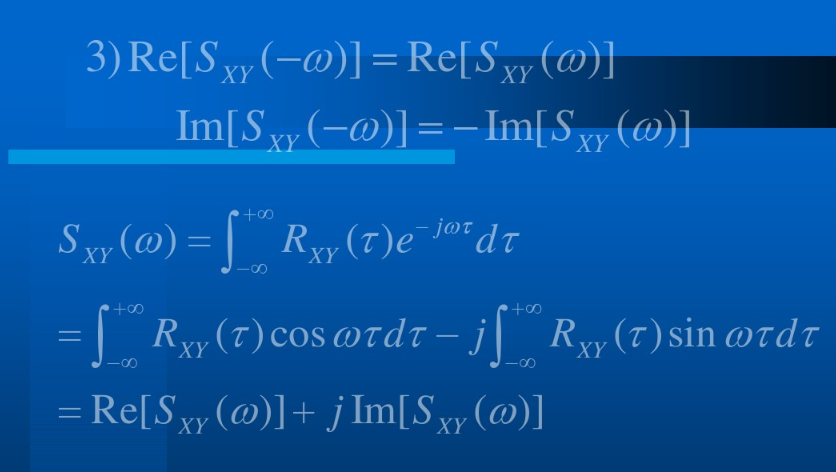
白噪声过程

均值为 0 的平稳过程
功率谱密度恒定 $S(\omega) = \frac{N_0}{2}, \omega \in (-\infty, +\infty)$ ， $N_0$ 表示单边功率谱密度，相当于冲激响应函数
维纳辛钦公式：
$\begin{aligned} R(\tau) &= \frac{1}{2\pi}\int_{-\infty}^{+\infty}\frac{N_0}{2}e^{j\omega\tau}d\omega \\ &= \frac{N_0}{2}\frac{1}{2\pi}2\pi\delta(\tau) \\ &= \frac{N_0}{2}\delta(\tau) \end{aligned}$

上面的式子中，用到了一个有意思的积分，那就是：

$\int_{-\infty}^{+\infty}e^{j\omega t}d\omega$

这其实与狄拉克 $\delta$ 函数, Dirac delta function的定义有微妙的关系。

狄拉克 $\delta$ 函数

定义

笼统地来说，δ 函数是在实数线上的一个函数，在原点上无限，在所有其他点上为零，

$\delta (x)={\begin{cases}+\infty ,&x=0\\0,&x\neq 0\end{cases}}$

并同时满足以下条件

$\int _{-\infty }^{\infty }\delta (x)\,dx=1.$

这只是一个概略的表述：δ 函数并不是一个严格意义上的函数，没有任何定义在实数集上的函数能满足以上的条件。更严谨地来说，δ 函数可以定义为分布或测度。

傅里叶积分中的应用

历史上 $\delta$ 函数的引入就是约瑟夫·傅里叶在傅里叶变换中发现的，后来被奥古斯丁·路易·柯西用指数函数表达了这一定理。

$\int_{-a}^{a} e^{j\omega t}d\omega=\frac{e^{j\omega t}}{jt}|_{-a}^{a}=\frac{e^{jta}-e^{-jta}}{jt}=\frac{2j\sin{ta}}{jt}=2a\frac{\sin{ta}}{ta}$

令 $a \to +\infty$ ，项 $\frac{\sin{ta}}{ta} = \pi\delta(ta) = \pi\frac{1}{a}\delta(t)$ ，其中 $\delta$ 就是狄拉克 $\delta$ 函数。参见 Relationship to the Dirac delta distribution。

最终我们有：

$\int_{-\infty}^{+\infty}e^{j\omega t}d\omega = 2\pi\delta(t)$

也就是说：

$\frac{1}{2\pi}\int_{-\infty}^{+\infty}e^{j\omega t}d\omega = \delta(t)$

这个公式的物理意义是：常数 1 与 $\delta(t)$ 互为傅里叶变换对。

值得注意的是，常数 1 的傅里叶变换也是 $\delta(t)$ ，可以通过将上式中的 $\omega$ 用 $-\omega'$ 代替，得到：

$\frac{1}{2\pi}\int_{-\infty}^{+\infty}e^{-j\omega' t}d(-\omega') = \delta(t)$

$\frac{1}{2\pi}\int_{-\infty}^{+\infty}e^{-j\omega' t}d(\omega) = \delta(t)$

白：前后序列不相关，都是相同的功率谱。

例题

已知平稳随机过程的自相关函数为 $R_{\tau} = \frac{A}{4} + Ae^{-\beta|\tau|}$ , 其中 $A > 0, \beta > 0, -\infty < \tau < +\infty$ ，求其功率谱密度。

根据维纳-辛钦定理，功率谱密度是自相关函数的傅里叶变换：

$\begin{aligned} S(\omega) &= \int_{-\infty}^{+\infty}R(t)e^{-j\omega t}dt \\ &= \int_{-\infty}^{+\infty}\frac{A}{4}e^{-j\omega t}dt + \int_{-\infty}^{+\infty}Ae^{-\beta|t|}e^{-j\omega t}dt \\ &= \frac{A}{4} \cdot 2\pi \delta(\omega) + \int_{-\infty}^{+\infty}Ae^{-\beta|t|-j\omega t}dt \\ &= \frac{A}{4} \cdot 2\pi \delta(\omega) + \int_{-\infty}^{0}Ae^{\beta t-j\omega t}dt + \int_{0}^{+\infty}Ae^{-\beta t-j\omega t}dt\\ &= \frac{A}{4} \cdot 2\pi \delta(\omega) + \int_{-\infty}^{0} \frac{1}{(\beta-j\omega)} Ae^{(\beta-j\omega) t}d[(\beta-j\omega) t] \\ & \quad -\frac{1}{(\beta +j\omega)}\int_{0}^{+\infty}Ae^{-(\beta +j\omega) t}d-[(\beta +j\omega)t]\\ &= \frac{A}{4} \cdot 2\pi \delta(\omega) + \frac{1}{(\beta-j\omega)} Ae^{(\beta-j\omega) t}\Big|_{t=-\infty}^{t=0} \\ & \quad -\frac{1}{(\beta +j\omega)}Ae^{-(\beta +j\omega) t}\Big|_{t=0}^{t=+\infty}\\ &= \frac{A}{4} \cdot 2\pi \delta(\omega) + \frac{1}{(\beta-j\omega)} A + \frac{1}{(\beta +j\omega)}A \\ &= \frac{\pi}{2}A\delta(\omega) + \frac{2A\beta}{\beta^2+\omega^2} \end{aligned}$

参考文献

众多维基百科条目。