行列式的物理（几何）意义、计算方式、拉普拉斯展开证明等等。

表示

方阵 $A$ 的行列式记为 $\det(A), \det A, |A|$。

意义

几何上表示方阵所表示的线性变换的缩放因子。

行列式可以看做是有向面积或体积的概念在一般的欧几里得空间中的推广。或者说，在 $n$ 维欧几里得空间中，行列式描述的是一个线性变换对“体积”所造成的影响。无论是在线性代数、多项式理论，还是在微积分学中（比如说换元积分法中），行列式作为基本的数学工具，都有着重要的应用。

定义

直观定义

$\det(A)=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)}$

• $S_n$: 集合 ${\displaystyle \left\{1,2,...,n\right\}}$ 上置换的全体，即集合 ${\displaystyle \left\{1,2,...,n\right\}}$ 到自身上的一一映射（双射）的全体，一共有 $A_{nn} = n!$ 个元素，，因此上式中共有 $n!$ 个求和项。$S_n$ 中每个元素 $\sigma$ 都是一个映射关系，给定一个输入 $i$，给出一个输出。

• ${\displaystyle \operatorname {sgn}(\sigma )}$ 表示置换 ${\displaystyle \sigma \in S_{n}}$ 的符号差，具体地说，满足 ${\displaystyle 1\leq i\leq j\leq n}$ 但 ${\displaystyle \sigma (i)>\sigma (j)}$ 的有序数对 ${\displaystyle \left(i,j\right)}$ 称为 ${\displaystyle \sigma }$ 的一个逆序。如果 $\sigma$ 的逆序共有偶数个，则 ${\displaystyle \operatorname {sgn} \sigma =1}$，如果共有奇数个，则 ${\displaystyle \operatorname {sgn} \sigma =-1}$。

  举例来说，对于 3 元置换 ${\displaystyle \sigma =\left(2,3,1\right)}$（即是说 ${\displaystyle \sigma (1)=2}，{\displaystyle \sigma (2)=3}， {\displaystyle \sigma (3)=1}$）而言，由于 1 在 2 后，1 在 3 后，所以共有 2 个逆序（偶数个），因此 ${\displaystyle \operatorname {sgn} (\sigma )=1}$，从而 3 阶行列式中项 ${\displaystyle a_{1,2}a_{2,3}a_{3,1}}$ 的符号是正的。

• $a_{ij}$: 矩阵 $A$ 的第 $i$ 行第 $j$ 列的元素

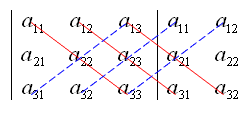
对于简单的 2 阶和 3 阶的矩阵，行列式的表达式相对简单，而且恰好是每条主对角线（左上至右下）元素乘积之和减去每条副对角线（右上至左下）元素乘积之和（见图中红线和蓝线）。

二阶方阵：

${\displaystyle {\begin{vmatrix}a_{1,1}&a_{1,2}\\a_{2,1}&a_{2,2}\end{vmatrix}}=a_{1,1}a_{2,2}-a_{1,2}a_{2,1}}$

三阶方阵：

$\displaystyle {\begin{vmatrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{vmatrix}} \\ =a_{1,1}a_{2,2}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2} \\ \quad -a_{1,3}a_{2,2}a_{3,1}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3}$

但对于阶数 ${\displaystyle n\geq 4}$ 的方阵 $A$，这样的主对角线和副对角线分别只有 $n$ 条，由于 $A$ 的主、副对角线总条数 ${\displaystyle =2n<\left(n-1\right)n<n!=S_{n}}$ 的元素个数 因此，行列式的相加项中除了这样的对角线乘积之外，还有其他更多的项。例如 4 阶行列式中，项 ${\displaystyle a_{1,2}a_{2,3}a_{3,1}a_{4,4}}$ 就不是任何对角线的元素乘积。不过，和 2、3 阶行列式情况相同的是，n 阶行列式中的每一项仍然是从矩阵中选取 n 个元素相乘得到，且保证在每行和每列中都恰好只选取一个元素，而整个行列式恰好将所有这样的选取方法遍历一次。

另外， $n\times n$ 矩阵的每一行或每一列也可以看成是一个 $n$ 元向量，这时矩阵的行列式也被称为这 $n$ 个 $n$ 元向量组成的向量组的行列式。

拉普拉斯展开（代数余子式展开法）

对一个 $n$ 阶的行列式 $M$，去掉 $M$ 的第 $i$ 行第 $j$ 列后形成的 $n-1$ 阶的行列式叫做 $M$ 关于元素 ${\displaystyle m_{ij}}$ 的余子式。记作 $M_{ij}$

$M_{ij}={\begin{vmatrix}m_{1,1}&\dots &m_{1,j-1}&m_{1,j+1}&\dots &m_{1,n}\\\vdots &&\vdots &\vdots &&\vdots \\m_{i-1,1}&\dots &m_{i-1,j-1}&m_{i-1,j+1}&\dots &m_{i-1,n}\\m_{i+1,1}&\dots &m_{i+1,j-1}&m_{i+1,j+1}&\dots &m_{i+1,n}\\\vdots &&\vdots &\vdots &&\vdots \\m_{n,1}&\dots &m_{n,j-1}&m_{n,j+1}&\dots &m_{n,n}\end{vmatrix}}$

$M$ 关于元素 ${\displaystyle m_{ij}}$ 的代数余子式记作 $C_{ij}$。 $C_{ij}=(-1)^{(i+j)}\cdot M_{ij}$。

一个 $n$ 阶的行列式 $M$ 可以写成一行（或一列）的元素与对应的代数余子式的乘积之和，叫作行列式按一行（或一列）的展开。

$\det {M}=\sum _{j=1}^{n}m_{ij}C_{i,j}, 按第 i 行展开 \\ det {M}=\sum _{i=1}^{n}m_{ij}C_{i,j}, 按第 j 列展开 \\$

这就是拉普拉斯公式，把 $n$ 维矩阵的行列式计算变为了 $n$ 个 $n-1$ 维的行列式的计算。另一方面，拉普拉斯公式可以作为行列式的一种归纳定义。可以证明这与第一种定义等价。

二阶方阵：

${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.\end{aligned}}}$

三阶方阵：

${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}\Box &\Box &\Box \\\Box &e&f\\\Box &h&i\end{vmatrix}}-b\,{\begin{vmatrix}\Box &\Box &\Box \\d&\Box &f\\g&\Box &i\end{vmatrix}}+c\,{\begin{vmatrix}\Box &\Box &\Box \\d&e&\Box \\g&h&\Box \end{vmatrix}}\\[3pt]&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\[3pt]&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}}$

四阶方阵：

${\displaystyle {\begin{vmatrix}a&b&c&d\\e&f&g&h\\i&j&k&l\\m&n&o&p\end{vmatrix}}=a\,{\begin{vmatrix}f&g&h\\j&k&l\\n&o&p\end{vmatrix}}-b\,{\begin{vmatrix}e&g&h\\i&k&l\\m&o&p\end{vmatrix}}+c\,{\begin{vmatrix}e&f&h\\i&j&l\\m&n&p\end{vmatrix}}-d\,{\begin{vmatrix}e&f&g\\i&j&k\\m&n&o\end{vmatrix}}.}$

证明：

从上面的定义开始：

$\begin{aligned} \det(M) &=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}m_{i,\sigma (i)} \end{aligned}$

就是要证明：

$\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}m_{i,\sigma (i)} = \sum_{j=1}^nm_{ij}C_{ij} = \sum_{j=1}^n(-1)^{i+j}m_{ij}M_{ij}$

考虑 $M$ 中每个含有 $m_{ij}$ 的项：

$\begin{aligned} & \operatorname{sgn} ({\tau}) \cdot m_{1, \tau(1)} \cdots m_{i, j}, \cdots m_{n, \tau(n)} \\ &= \operatorname{sgn}(\tau) \cdot m_{ij} \cdot m_{1, \tau(1)} \cdots m_{i-1, \tau(i-1)}m_{i+1, \tau(i+1)} \cdots m_{n, \tau(n)} \\ &\xlongequal{记 M_{ij} 的元素为 a_{st}} \operatorname{sgn}(\tau) \cdot m_{ij} \cdot a_{1, \sigma(1)} \cdots a_{i-1, \sigma(i-1)}a_{i, \sigma(i)} \cdots a_{n-1, \sigma(n-1)} \\ \end{aligned}$

显然，每个 τ 都对应着唯一的 σ，每一个 σ 也对应着唯一的 τ。因此我们创建了 $S_{n − 1}$ 与 $\{τ ∈ S_n : τ(i) = j\}$ 之间的一个双射。置换 τ 可以经过如下方式从 σ 得到：

定义 $σ' ∈ S_n$使得对于 $1 ≤ k ≤ n − 1，σ'(k) = σ(k)$ 并且 $σ'(n) = n$，于是 $\operatorname{sgn} (σ') = \operatorname{sgn} (σ)$。然后：

${\displaystyle \tau \,=(n,n-1,\ldots ,i)\,\sigma '\,(j,j+1,\ldots ,n)}。$

这个乘积可以按如下的方式进行理解，从上到下表示映射关系：

$\begin{pmatrix} n & n-1 & n-2 & \cdots & i+1 & i \\ n-1 & n-2 & n-3 & \cdots & i & n \\ \sigma'(n-1) & \sigma'(n-2) & \sigma'(n-3) & \cdots & \sigma'(i) & n \\ \begin{cases} \sigma'(n-1), \sigma'(n-1) < j \\ \sigma'(n-1)+1, \sigma'(n-1) \ge j \\ \end{cases} & \begin{cases} \sigma'(n-2), \sigma'(n-2) < j \\ \sigma'(n-2)+1, \sigma'(n-2) \ge j \\ \end{cases} & \begin{cases} \sigma'(n-3), \sigma'(n-3) < j \\ \sigma'(n-3)+1, \sigma'(n-3) \ge j \\ \end{cases} & \cdots & \begin{cases} \sigma'(i), \sigma'(i) < j \\ \sigma'(i)+1, \sigma'(i) \ge j \\ \end{cases} & j \end{pmatrix}$

也就是说经过从 $\sigma'$ 变为 $\tau$，其余映射关系不变。由于删除了 $m_{ij}$ 项，大于 $i$ 的自变量 $t$ 变换结果会会是 $\sigma'(t-1) + \delta, \delta = 1\ \text{when}\ \sigma'(t-1) \ge j$。

由于两个轮换分别可以被写成 $n − i$ 和 $n − j$ 个对换，因此

${\displaystyle \operatorname {sgn} (\tau) \,=(-1)^{2n-(i+j)}\operatorname {sgn} (\sigma) '\,=(-1)^{i+j}\operatorname {sgn} (\sigma) }$

现在只考虑行列式展开中 $\tau(i) = j$ 的那些项数：

$\begin{aligned} \sum _{\tau \in S_{n}, \tau(i) = j}\operatorname {sgn}(\tau )\prod _{i=1}^{n}m_{i,\tau (i)} &= \sum_{\sigma \in S_{n-1}} (-1)^{i+j}\operatorname {sgn} \sigma \cdot m_{ij} \cdot a_{i, \sigma(1)} \cdots a_{n-1, \tau(n-1)} \\ &= (-1)^{i+j} m_{ij}M_{ij} \end{aligned}$

再对所有的 $j$ 作和

$\det(A) = \sum_{j=1}^n \left( \sum _{\tau \in S_{n}, \tau(i) = j}\operatorname {sgn}(\tau )\prod _{i=1}^{n}m_{i,\tau (i)} \right) = \sum_{j=1}^n (-1)^{i+j} m_{ij}M_{ij} = \sum_{j=1}^n m_{ij}C_{ij}$

这也就证明了按第 $i$ 行展开的正确性。

应用

线性方程组求解

行列式概念最早出现在解线性方程组的过程中。十七世纪晚期，关孝和与莱布尼茨的著作中已经使用行列式来确定线性方程组解的个数以及形式。十八世纪开始，行列式开始作为独立的数学概念被研究。十九世纪以后，行列式理论进一步得到发展和完善。矩阵概念的引入使得更多有关行列式的性质被发现，行列式在许多领域都逐渐显现出重要的意义和作用，出现线性自同态和向量组的行列式的定义。

矩阵可逆

TODO

特征多项式

TODO

平行六面体

TODO

范德蒙德恒等式

TODO

参考文献

1. Determinant | Wikipedia
2. 拉普拉斯展开 | 维基百科